Rumus Penjumlahan Aljabar – Materi Kuliah Rumus penjumlahan aljabar dan pengurangan aljabar sama halnya dengan penjumlahan ataupun pengurangan bentuk bilangan bulat . Aljabar merupakan salah satu cabang aritmatika dalam ilmu matematika yang ditemukan oleh ilmuwan arab yang bernama ” Abu Abdullah Muhamad ibnu Musa Al Khawarizi ” . Aljabar memiliki arti suatu cara untuk menyelesaikan atau memecahkan suatu masalah .
Macam – Macam bentuk aljabar
Aljabar di bagi dalam 5 macam , yaitu :
1. Aljabar elementer ( aljabar dasar ) , yaitu bentuk aljabar untuk menyelesaikan bilangan riil yang menggunakan peubah untuk menandakan variabel dan konstanta.
2. Aljabar Linier
3. Aljabar Abstrak
4. Aljabar Universal
5. Aljabar komputer
Istilah – istilah yang perlu di fahami dalam bentuk aljabar
Istilah – istilah ini merupakan unsur – unsur yang terdapat dalam bentuk aljabar , unsur – unsur tersebut adalah :
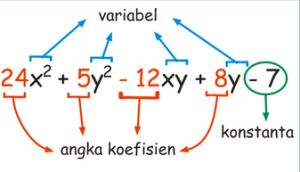
1. Variabel disebut juga dengan peubah , yang memiliki pengertian lambang pengganti bilangan yang belum di ketahui . Contoh variabel : x , y , a , b , xy
2. Koefisien yaitu angka yang terdapat di depan variabel .
contoh : x+3 = koefisiennya adalah 1 , 3x+5 = koefisiennya adalah 3
3. Konstanta ,yaitu suku dari suatu bentuk aljabar yang berdiri sendiri
contoh : 4x + 5y + 6 , maka konstanta dari bentuk aljabar tersebut adalah 6
4. Suku , yaitu nilai yang menyusun suatu bentuk aljabar yang berupa variabel , koefisien ataupun konstanta .
macam – macam suku :
1. Menurut jenisnya :
- Suku sejenis , yaitu bentuk aljabar yang variabel dan pangkatnya sama contoh : 3x dan x , 3xy dan xy
- suku tak sejenis , yaitu bentuk aljabar yang variabel dan pangkatnya tak sama .contoh : 4x dan 4y , 2xy dan 3xy2 , 2xy dan x
2. Menurut jumlah sukunya :
- suku satu , yaitu bentuk aljabar yang berdiri sendiri yang tidak dihubungkan oleh operasi penjumlahan ataupun selisih . contoh x , 2x
- suku dua , yaitu bentuk aljabar yang dihubungkan oleh operasi penjumlahan ataupun selisih . contoh: x+y , 3x- y
- suku tiga , yaitu bentuk aljabar yang dihibungkan oleh 2 operasi penjumlahan ataupun selisih . contoh : x+y+7, 2x+2xy+2
Operasi bentuk aljabar
operasi hitung dalam aljabar , sama halnya dengan operasi hitung bilangan bulat yaitu meliputi :
1. Penjumlahan bentuk aljabar
2. Pengurangan bentuk aljabar
3. Perkalian bentukaljabar
4. Pembagian bentuk aljabar
5. Perpangkatan bentuk aljabar
Dalam kesempatan kali ini , kita akan mempelajari penjumlahan dan pengurangan aljabar .
Penjumlahan dan Pengurangan Bentuk Aljabar
Bentuk aljabar yang dapat dijumlahkan atau dikurangkan yaitu hanya pada bentuk aljabar yang memiliki suku yang sama . Dalam penjumlahan dan pengurangan yang dijumlah ataupun dikurangkan adalah koefisiennya dalam suku yang sama .
Penjumlahan Bentuk Aljabar
Pengurangan Bentuk Aljabar
Keterangan :
a dan b = koefisien
n = Variabel
Contoh soal
1. Tentukan koefisien dari bentuk – bentuk aljabar berikut :
a. 2x2 + x – 1
b. 3x2 +- 2x + 1
c. x2 + 5x – 6
d. ax3 + bx2 + cx + d
Jawab :
a. koefisien x2 = 2 dan x = 1
b. koefisien x2 = 3 dan x = 2
c. koefisien x2 = 1 dan x = 5
d. koefisien x3 = a , x2 = b dan x = c
2. Sederhanakan bentuk aljabar berikut :
a. 3x2 – 4 x2 + 7x – 2 x + 1
b. 4x2 – 2y + 1 – 5x2 + x + y
c. 4 ( 2x2 – y ) + 3 ( x2 + y )
Jawab :
a. 3x2 – 4 x2 + 7x – 2 x + 1
= ( 3 – 4 ) x2 + ( 7 – 2 )x + 1
= -1 x2 + 5x + 1
b. 4x2 – 2y + 1 – 5x2 + x + y
= (4 – 5 )x2 – ( 2 + 1 ) y + 1 + x
= -1x2 – 3y +1 + x
c. 4 ( 2x2 – y ) + 3 ( x2 + y )
= ( 4 + 3 ) + ( 2 + 1 ) x2 + ( -y + y )
= 7 + 3x2 – y + y
3. Tentukan suku – suku sejenis dari pasangan berikut :
a. x2 + 2x2 – 1 dengan 3x2 + x +xy
b. 2x2 + x dengan –x2 +2
c. -2x +5 dengan 5x2 -2
d. x3 – x2 dengan 4x2 + x
Jawab :
a. x2 + 2x – 1 dengan 3x2 + x +xy
suku – suku yang sejenis adalah : x2 dan 3x2 , 2x dan x
b. 2x2 + x dengan –x2 +2
suku – suku yang sejenis adalah : 2x2 dan –x2
c. -2x +5 dengan 5x2 -2
suku – suku yang sejenis adalah : s dan -2
d. x3 – x2 dengan 4x2 + x
suku – suku yang sejenis adalah : – x2 dan 4x2
4. Tentukan penjumlahan dari bentuk aljabar berikut :
a. 4x + x
b. 5xy + 6xy
c. 3xy + 3 + 4xy +1
d. ( 3x + 4xy + 2 ) + ( 3 + 4x + 2xy )
Jawab :
a. 4x + x = 5x
b. 5xy + 6xy = 11xy
c. 3xy + 3 + 4xy +1
= ( 3 + 4 ) xy + ( 3 + 1 )
= 7xy + 4
d. ( 3x + 4xy + 2 ) + ( 3 + 4x + 2xy )
= 3x + 4xy + 2 + 3 + 4x + 2xy
= ( 3x + 4x ) + ( 4xy + 2xy ) + ( 2 + 3 )
= 7x + 6xy + 5
5. Tentukan hasil pengurangan dari bentuk aljabar berikut :
a. 5xy – xy
b. 3y – 5y
c. -x – 4x
Jawab :
a. 5xy – xy = 4 xy
b. 3y – 5y = -2y
c. -x -4x = -5x
6. Tentukan hasil dari penjumlahan dan pengurangan dari bentuk aljabar berikut :
a. -2x2 + 5x2
b. ( -5 x3 + 4x2 -7 ) + ( x2 -x + 4 )
c. ( 3p3 – 2aq2 + 5 ) – ( p2 – aq2 -10 )
d. 3x2 – 4x2 + 7x – 2x +1
Jawab :
a. -2x2 + 5x2
= ( -2 + 5 ) x2
= 3 x2
b. ( -5 x3 + 4x2 -7 ) + ( x2 -x + 4 )
= -5 x3+ ( 4 + 1 )x2 – x + ( -7 + 4 )
= -5 x3 + 5x2 – x -3
c. ( 3p3 – 2aq2 + 5 ) – ( p2 – aq2 -10 )
= 3p3 – p2 – ( 2 – 1 ) aq2 + ( 5 – 10 )
= 3p3 – p2 – aq2 -5
d. 3x2 – 4x2 + 7x – 2x +1
= ( 3 – 4 ) x2 + ( 7 – 2 ) x + 1
= -1 x2 – 5x + 1
Demikian penjelasan mengenai rumus penjumlahan dan pengurangan bentuk aljabar . Kunci untuk menyelesaikan sebuah permasalahan dari bentuk aljabar khususnya penjumlahan dan pengurangan yaitu memahami suku – suku yang sejenis dan pangkatnya sama . Setelah kita memahami itu semua , maka pemahaman tentang penjumlahan dan pengurangan dapat kita langsung kita aplikasikan ke dalamnya . Sesungguhnya sesuatu yang terlihat sulit , apabila kita serius dalam berlatih dan berusaha memahaminya itu semua dapat berubah menjadi hal yang sangat mudah .

EmoticonEmoticon